Модели разделенной выживаемости (partitioned survival models) в настоящее время очень часто используются в оценке технологий здравоохранения для выполнения анализа «затраты-эффективность». Их преимущества и недостатки вне рамок данной статьи, они подробно изложены в различных источниках, например в «методических рекомендациях» NICE DSU (National Institute for Health and Care Excellence) – Technical Support Document 19.
Для построения таких моделей необходимо иметь индивидуальные данные пациентов (individual patient data), как минимум – в какой группе находился пациент (получал терапию или плацебо), его статус в отношении критерия эффективности (наступило или не наступило событие конечной точки) в момент времени нахождения исследования. Как правило, доступ к таким данным ограничен. Однако, существуют методы, позволяющие восстанавливать (имитировать) индивидуальные данные пациентов из опубликованных результатов исследований в виде кривой Каплана-Мейера (Guyot, P., Ades, A., Ouwens, M.J. et al. Enhanced secondary analysis of survival data: reconstructing the data from published Kaplan-Meier survival curves. BMC Med Res Methodol 12, 9 (2012). https://doi.org/10.1186/1471-2288-12-9).
Первым этапом восстановления индивидуальных данных пациентов является оцифровка опубликованной кривой Каплан-Мейера – получения координат (x, y) кривой, где x – время, y – доля пациентов, достигших (или наоборот, не достигших) исхода (события конечной точки). Именно эту процедуру мы рассмотрим в рамках этой статьи.
Нам потребуется вспомогательный софт для оцифровки графиков, который упростит получение координат (x, y). По запросу «plot digitizer» в Гугле вы найдете множество подобных утилит. Я пользуюсь программой WebPlotDigitizer, она бесплатна и достаточно функциональна. В этой статье я буду использовать именно эту программу.
Также нам потребуется кривая Каплан-Мейера из статьи с результатами исследования. В моем примере используются данные об общей выживаемости из клинического исследования лекарственного препарата нусинерсен, который применяется для лечения детей со спинальной мышечной атрофией (СМА). Публикация размещена на сайте журнала The New England Journal of Medicine.
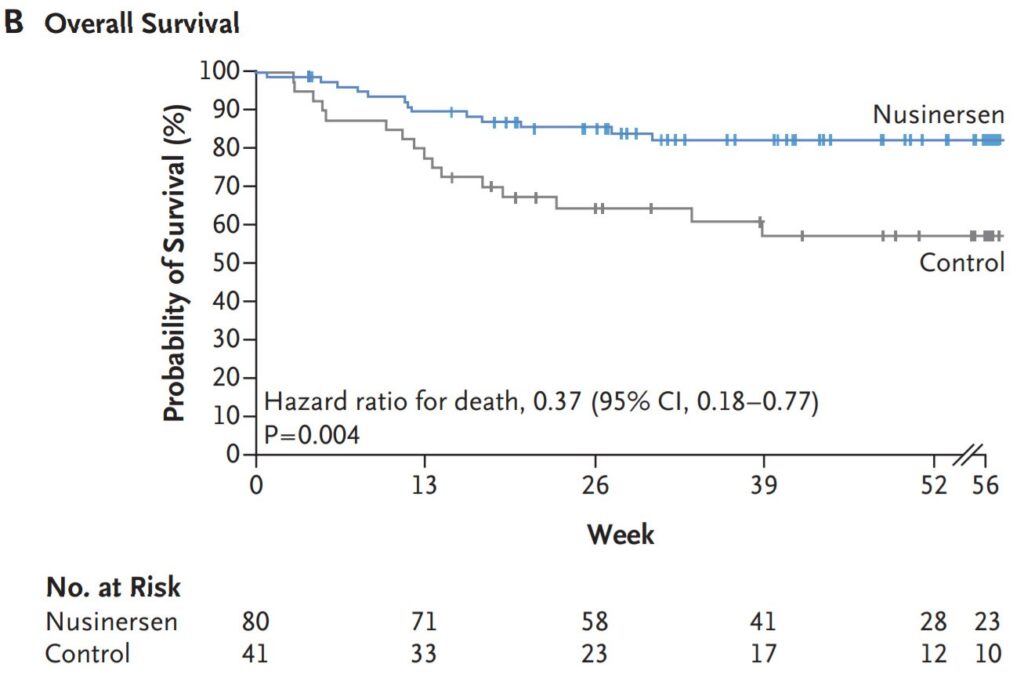
Для того, чтобы «вырезать» график с общей выживаемостью из статьи можно использовать встроенную в Windows функцию, нажав комбинацию клавиш «Win+Shift+S». После этого, загрузите график в программу WebPlotDigitizer.
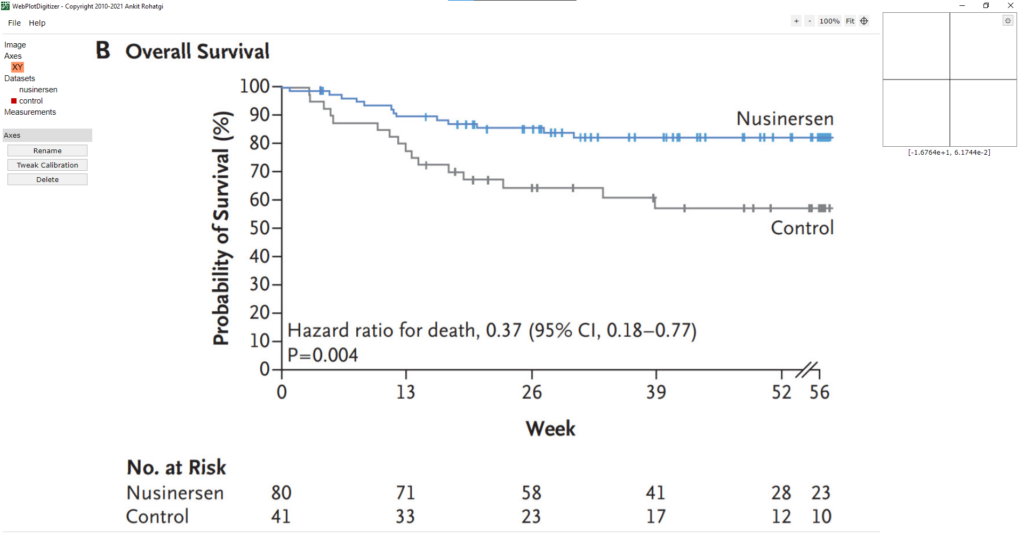
Сразу после загрузки графика, появится окно в котором необходимо указать тип графика – выбираем 2D (X-Y) Plot.
После этого выполняем калибровку осей X-Y в следующем порядке:
- X1 – пересечение осей X и Y – нулевое значение на графике
- X2 – 52 неделя (обратите внимание, что всего на графике 56 недель, но период 52-56 недели вне масштаба графика, поэтому нужно выбирать именно 52 неделю, в противном случае ось Х будет откалибрована неправильно)
- Y2- 100%
В итоге оси должны быть откалиброваны следующим образом:
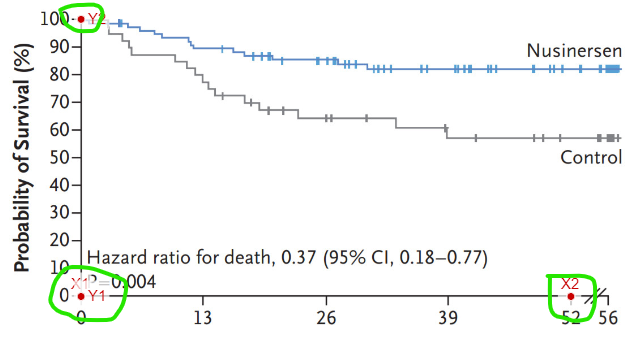
Теперь приступим к нанесению координат кривой нусинерсена. Чтобы программа не выдавала точки вне кривой, ограничим ее работу необходимой зоной с помощью инструмента Pen – желтая полоса на рисунке ниже.
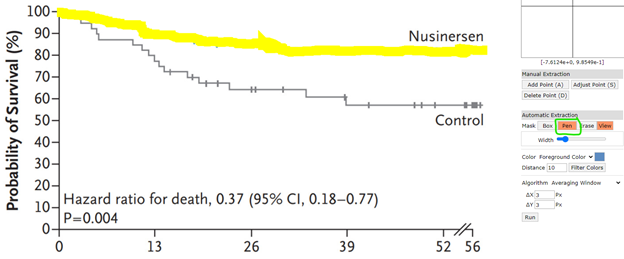
С помощью пипетки укажем цвет необходимой кривой.
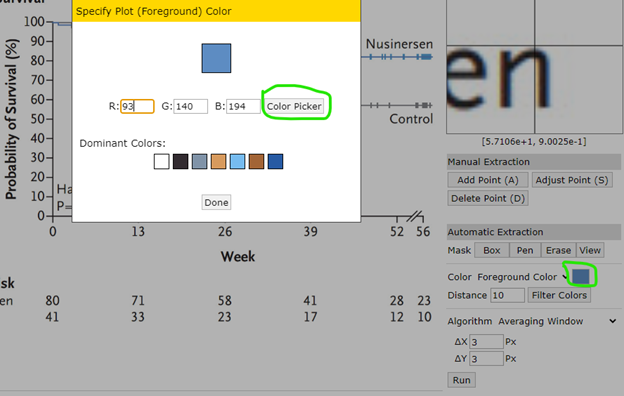
После этого нажимаем кнопку Run и программа автоматически проставит точки на кривой нусинерсена. Наша задача получить точки, которые как можно более точно соответствуют кривой, самое главное отследить места, где кривая «движется» вниз – в дальнейшем существенно повлияет на результаты.
С первого раза, как правило, не получается добиться необходимого результата и нужно поработать с настройками алгоритма:
- Distance – отклонение от заданного (с помощью пипетки ранее) цвета. Нажав на Filter Color вы увидите какие участки кривой алгоритм будет использовать
- Δ X и Y – шаг алгоритма в пикселях по горизонтали и по вертикали. Чем меньше шаг, тем больше точек Вы получите.
Также, можно добавить, удалить и изменить положение точек самостоятельно – рабочая панель справа Manual Extraction.
Помните — самое главное отследить места, где кривая «движется» вниз – в дальнейшем существенно повлияет на результаты. Это очень важная часть восстановления данных, базис на которой в дальнейшем будет построена модель.
Однако, для наших целей не будем тратить на этом этапе много времени. В итоге, вот что у меня получилось. Черные точки – нусинерсен, красные точки – контроль.
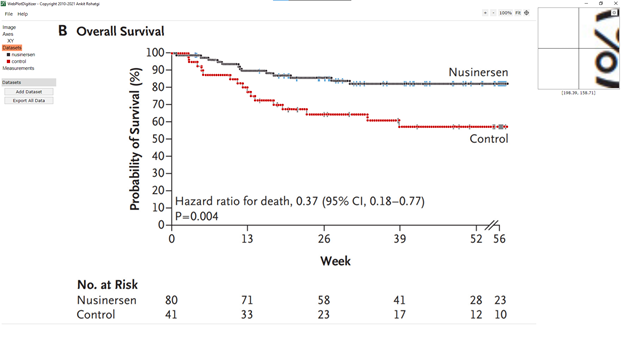
Теперь экспортируем данные в Эксель, для этого на рабочей панели слева выбираем Datasets, затем Export All Data и Download .CSV.
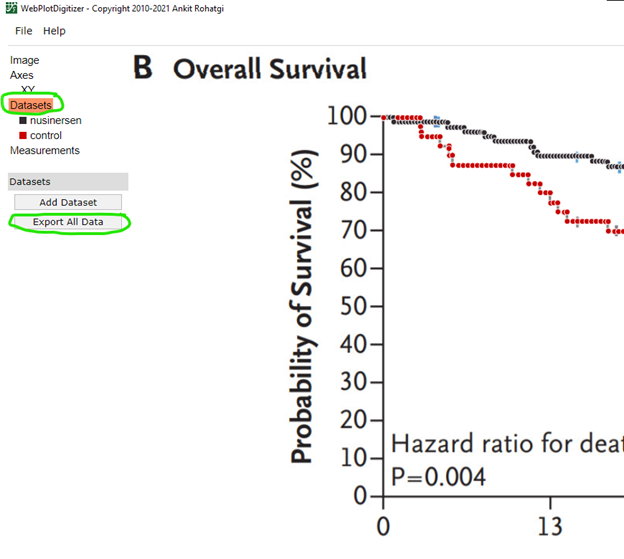
В Эксель будет необходимо данные, которые у нас находятся в одном столбце, разделенные запятыми, перенести в четыре столбца – для этого удобно использовать функцию «Данные – Текст по столбцам». Дайте столбцам следующие названия (это важно, т.к. в дальнейшем в программе R-Studio мы будем использовать именно эти названия):
- нусинерсен время — arm1_time
- нусинерсен доля живых пациентов — arm1_status
- время — arm0_time
- контроль доля живых пациентов — arm0_status
Добавим еще три столбца, которые нам понадобятся дальше, при восстановлении данных:
- временные отметки для которых есть данные о количестве пациентов под риском – trisk
- нусинерсен пациенты под риском — nrisk_arm1
- контроль пациенты под риском — nrisk_arm1
Эти данные приведены под графиком в публикации.

В итоге, должна получится такая шапка таблицы:

В первой строке я указал самостоятельно время -0, доля – 1, т.к. все пациенты были живы в начале исследования.
Помните, что период 52-56 неделя по оси X имеет отличающийся масштаб? Проверьте свои данные, удалите данные с временем больше 56 недели. Сохраните файл с именем «dataset.xlsx».
Итак, мы с Вами сделали первый и очень важный этап на пути восстановления (имитации) индивидуальных данных пациентов в клиническом исследовании – получили координаты кривых Каплана-Мейера. И уже сейчас мы можем анализировать полученные данные, например, рассчитать разницу абсолютных рисков в различное время в исследовании. И в следующем материале мы на основании восстановленных данных выполним регрессию по Коксу и сравним полученное значение Hazard Ratio (HR) и сравним его с опубликованным. Интересно, насколько сильно они будут отличаться и будут ли?
Ниже приложил два файла:
Дорогой читатель, буду рад твоим комментариям, предложениям и вопросам!