В этом материале мы рассмотрим два практических примера выполнения непрямых сравнений c коррекцией популяций: согласованное непрямое сравнение (Matching-adjusted Indirect Comparisons – MAIC) и симуляционное сравнение (Simulated Treatment Comparisons — STC). Данные методы сравнения позволяют снизить уровень неопределенности результатов, обусловленной различием характеристик популяций пациентов в исследованиях. Подробное изучение данных методов можно начать с TSD 18 NICE DSU. Основной задачей этого материала является выполнение практических примеров в программной среде R.
Для выполнения MAIC и STC необходимо наличие данных на уровне характеристик и исходов каждого пациента для исследуемого вмешательства, к которым доступ, как правило, отсутствует. Однако, учитывая, увеличение количества исследования такого рода, в том числе опубликованных в научных статьях, практическое представление процессов MAIC и STC представляется полезным, особенно в случае выполнения клинико-экономических исследований на базе результатов MAIC и STC.
При воспроизведении всех вышеуказанных процедур в R вы получите отличающиеся результаты от представленных в материале. Это обусловлено тем, что генерация популяций пациентов происходит случайном образом в заданных пределах. В свою очередь, это повлияет на генерацию исходов.
MAIC
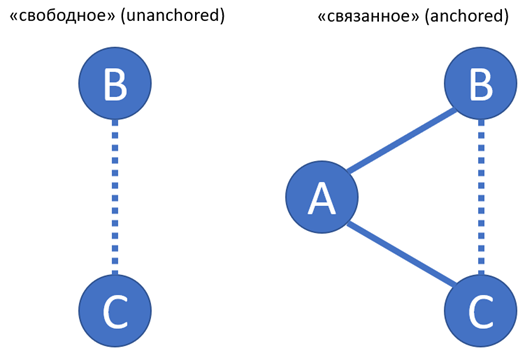
MAIC может быть «свободным» (unanchored) или «связанным» (anchored). Последнее является предпочтительным, однако, в случае отсутствия возможности построения сети сравнения, возможно применение «свободного» MAIC. В данном материале представлен пример anchored MAIC «B» в сравнении с «С» из TSD 18 NICE DSU. Пример unanchored MAIC будет разобран в другом материале, где мы рассмотрим подключаемую в R библиотеку maic.
Для начала установим и загрузим необходимые библиотеки:
if(!require(dplyr)) {install.packages("dplyr"); library(dplyr)}
if(!require(tidyr)) {install.packages("tidyr"); library(tidyr)}
if(!require(wakefield)) {install.packages("wakefield"); library(wakefield)}
if(!require(ggplot2)) {install.packages("ggplot2"); library(ggplot2)}
if(!require(sandwich)) {install.packages("sandwich"); library(sandwich)}
Далее, создадим данные для выполнения MAIC с помощью библиотеки wakefield, которая позволяет быстро создавать реалистичные наборы данных. В первую очередь зададим характеристики исследований:
# Харатеристики исследований
N_AB <- 500 # кол-во пациентов в исследовании АВ
N_AC <- 300 # кол-во пациентов в исследовании АС
agerange_AB <- 45:75 # диапазон возрастов пациентов в исследовании АВ
agerange_AC <- 45:55 # диапазон возрастов пациентов в исследовании АВ
femalepc_AB <- 0.64 # доля женщин в исследовании АВ
femalepc_AC <- 0.8 # доля женщин в исследовании АС
Для модели исходов будем использовать логистическую регрессию, в которой вероятность исхода (yprob) будет рассчитана по формуле:
yprob = 1 / (1 + exp(-(b_0 + b_gender * (gender == "Male") + b_age * (age - 40) + (b_trt_B + b_age_trt * (age - 40))
Задаем переменные с коэффициентами регрессионной модели исходов:
# Модель исходов исследований АВ и АС
b_0 <- 0.85 # intercept
b_gender <- 0.12 # коэффициент пола
b_age <- 0.05 # коэффициент возраста
b_age_trt <- -0.08 # коэффициент взаимодействия (в случае терапии)
b_trt_B <- -2.1 #коэффицент вмешательства В
b_trt_C <- -2.5 #коэффицент вмешательства С
Генерируем рукава исследования АВ:
AB.IPD <-
rbind(
# Создаем рукав А с помощью функции r_data_frame библиотеки wakefield
r_data_frame(n = N_AB/2, # кол-во пациетов в рукаве А
id, # уникальный номер ID
age = age(x = agerange_AB), # генерируем возраста
gender = gender(prob = c(1 - femalepc_AB, femalepc_AB)), # генерируем пол
trt = "A" # присваиваем лейбл вмешательства А
),
# Создаем рукав В с помощью функции r_data_frame библиотеки wakefield
r_data_frame(n = N_AB/2, # кол-во пациетов в рукаве В
id, # никальный номер ID
age = age(x = agerange_AB), # генерируем возраста
gender = gender(prob = c(1 - femalepc_AB, femalepc_AB)), # генерируем пол
trt = "B" # рисваиваем лейбл вмешательства В
)
) %>%
# Создаем исходы вмешательств, используя логистическую модель, где yprob - вероятность наступления исхода
mutate(
yprob = 1 / (1 + exp(-(
b_0 + b_gender * (gender == "Male") + b_age * (age - 40) +
if_else(trt == "B", b_trt_B + b_age_trt * (age - 40), 0)
))), # уравнение логистической регрессии
y = rbinom(N_AB, 1, yprob) # эта функция "конвертирует" вероятность исхода в собственно исход 1-да, 0-нет,
# с помомощью биномиального распределения
) %>%
select(-yprob) # удаляем колонку [yprob]
Смотрим в таблице сгенерированные исходы исследования АВ:
AB.IPD %>% group_by(trt) %>%
summarise(n(), mean(age), sd(age), `n(male)`=sum(gender=="Male"),
`%(male)`=mean(gender=="Male"), sum(y), mean(y))
trt `n()` `mean(age)` `sd(age)` `n(male)` `%(male)` `sum(y)` `mean(y)`
<chr> <int> <dbl> <dbl> <int> <dbl> <int> <dbl>
1 A 250 60.3 8.82 80 0.32 223 0.892
2 B 250 60.5 8.82 79 0.316 28 0.112
Генерируем рукава исследования АС:
AC.IPD <-
rbind(
r_data_frame(n = N_AC/2,
id,
age = age(x = agerange_AC),
gender = gender(prob = c(1 - femalepc_AC, femalepc_AC)),
trt = "A"
),
r_data_frame(n = N_AC/2,
id,
age = age(x = agerange_AC),
gender = gender(prob = c(1 - femalepc_AC, femalepc_AC)),
trt = "C"
)
) %>%
mutate(
yprob = 1 / (1 + exp(-(
b_0 + b_gender * (gender == "Male") + b_age * (age - 40) +
if_else(trt == "C", b_trt_C + b_age_trt * (age - 40), 0)
))),
y = rbinom(N_AC, 1, yprob)
) %>%
select(-yprob)
Смотрим в таблице сгенерированные исходы исследования АВ:
AC.IPD %>% group_by(trt) %>%
summarise(n(), mean(age), sd(age), `n(male)`=sum(gender=="Male"),
`%(male)`=mean(gender=="Male"), sum(y), mean(y))
trt `n()` `mean(age)` `sd(age)` `n(male)` `%(male)` `sum(y)` `mean(y)`
<chr> <int> <dbl> <dbl> <int> <dbl> <int> <dbl>
1 A 150 50.1 3.14 24 0.16 123 0.82
2 C 150 49.6 2.91 29 0.193 14 0.0933
Так как при проведении MAIC у нас есть в наличие только суммированные данные об исследовании АС, выполняем суммирование сгенерированных данных для АС:
AC.AgD <-
cbind(
# Рассчитываем среднее значени и СО возраста (age.mean и age.sd), кол-во и долю мужчин (N.male и prop.male)
summarise(AC.IPD, age.mean = mean(age), age.sd = sd(age),
N.male = sum(gender=="Male"), prop.male = mean(gender=="Male")),
# Суммируем исходы в рукаве А
filter(AC.IPD, trt == "A") %>%
summarise(y.A.sum = sum(y), y.A.bar = mean(y), N.A = n()),
# Суммируем исходы в рукаве А
filter(AC.IPD, trt == "C") %>%
summarise(y.C.sum = sum(y), y.C.bar = mean(y), N.C = n())
)
AC.AgD
age.mean age.sd N.male prop.male y.A.sum y.A.bar N.A y.C.sum y.C.bar N.C
1 49.83 3.036197 53 0.1766667 123 0.82 150 14 0.09333333 150
Подведем промежуточный итог, на данном этап мы сгенерировали индивидуальные данные (характеристики популяций пациентов и исходы) для исследований АВ и АС, сделали обобщение данных исследования АС. Теперь переходим непосредственно к MAIC. Первый этап будет заключаться в создании логистической модели (logistic propensity score model), которая позволит «взвесить» модификаторы исхода (в нашем случае это только возраст пациента – среднее значение и стандартное отклонение) в исследовании АВ, с помощью алгоритма минимизации настроить индивидуальные «веса» пациентов в исследовании таким образом, чтобы среднее взвешенное значение и стандартное отклонение возраста пациентов (модификатор эффекта) в исследовании АВ соответствовало суммированным данным исследования. Подробное описание процессов находится вне задача данного материла, с ними можно ознакомиться в публикации David M. Phillippo et al.
Зададим две функции, которые необходимы для алгоритма минимизации:
objfn <- function(a1, X){
sum(exp(X %*% a1))
}
gradfn <- function(a1, X){
colSums(sweep(X, 1, exp(X %*% a1), "*"))
}
X.EM.0 <- sweep(with(AB.IPD, cbind(age, age^2)), 2,
with(AC.AgD, c(age.mean, age.mean^2 + age.sd^2)), '-')
# алгоритм минимизации
print(opt1 <- optim(par = c(0,0), fn = objfn, gr = gradfn, X = X.EM.0, method = "BFGS"))
a1 <- opt1$par
# оцениваем вес для каждого индивидуального значения
wt <- exp(X.EM.0 %*% a1)
wt.rs <- (wt / sum(wt)) * N_AB # перекалибровки весов для удобной визуальной оценки
summary(wt.rs) # итоги "взвешивания"
V1
Min. :0.000000
1st Qu.:0.000007
Median :0.018620
Mean :1.000000
3rd Qu.:2.133576
Max. :4.046807
qplot(wt.rs, geom="histogram",
binwidth=0.25)
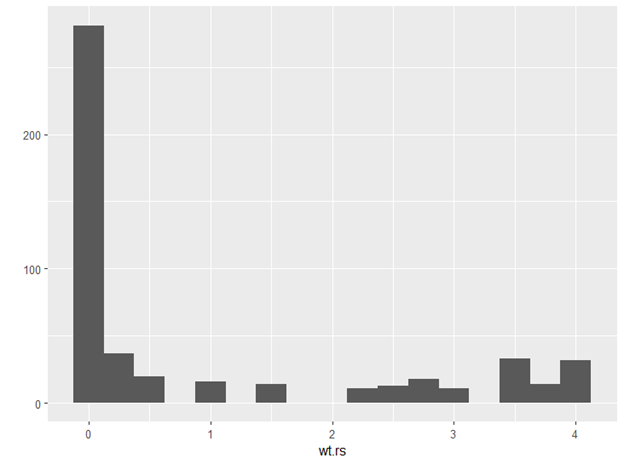
«Веса» находятся в интервале от 0 до 4,05, медиана резко смещена влево, что означает, что большое количество пациентов получило «вес» = 0, это объясняется тем, что возраста пациентов в исследовании АВ находятся в интервале 45-75 лет, в исследовании АС – 45-55 лет. Поэтому, большое количество пациентов исследования АВ было исключено (получило «вес» = 0).
Размер эффективного сэмпла составляет:
sum(wt)^2/sum(wt^2)
[1] 160.3545
Достаточно существенное сокращение от исходного количества пациентов – 500. Также обратим внимание, что возраст (среднее значение и СО) в исследовании АВ после взвешивания соответствует средним значениям исследования АС:
AB.IPD %>%
mutate(wt) %>%
summarise(age.mean = weighted.mean(age, wt),
age.sd = sqrt(sum(wt / sum(wt) * (age - age.mean)^2))
)
age.mean age.sd
<dbl> <dbl>
1 49.8 3.04
AC.AgD[, c("age.mean", "age.sd")]
age.mean age.sd
1 49.83 3.036197
Теперь рассчитаем эффект «В» в сравнении с «А» с учетом результатов «взвешивания»:
# Binomial GLM
fit1 <-
AB.IPD %>% mutate(y0 = 1 - y, wt = wt) %>%
glm(cbind(y,y0) ~ trt, data = ., family = binomial, weights = wt)
# Sandwich estimator of variance matrix
V.sw <- vcovHC(fit1)
# The log OR of B vs. A is just the trtB parameter estimate,
# since effect modifiers were centred
print(d.AB.MAIC <- coef(fit1)["trtB"]) # эффект «В» в сравнении с «А»
trtB
-3.645357
print(var.d.AB.MAIC <- V.sw["trtB","trtB"]) # дисперсия
[1] 0.2256259
И, финальный этап, выполняем непрямое сравнение:
# Estimated log OR of C vs. A from the AC trial
d.AC <- with(AC.AgD, log(y.C.sum * (N.A - y.A.sum) / (y.A.sum * (N.C - y.C.sum))))
var.d.AC <- with(AC.AgD, 1/y.A.sum + 1/(N.A - y.A.sum) + 1/y.C.sum + 1/(N.C - y.C.sum))
# Indirect comparison
print(d.BC.MAIC <- d.AC - d.AB.MAIC)
trtB
-0.1445882
print(var.d.BC.MAIC <- var.d.AC + var.d.AB.MAIC)
[1] 0.3495745
print(sqrt(var.d.BC.MAIC <- var.d.AC + var.d.AB.MAIC))
[1] 0.5912482
Таким образом, в результате MAIC получены следующие результаты:
- Эффект «С» в сравнении с «В» — logOR = -0.1445882
- Стандартная ошибка среднего — 0.5912482
STC
Переходим к этапу проведения симуляционного сравнения (STC) на ранее сгенерированных данных. Принципиально идея STC заключается в следующем: при наличии данных об исходах на уровне каждого пациента с исследовании АВ мы можем создать регрессионную модель зависимости исхода от модификаторов эффекта (в нашем случае возраст и пол) и использовать ее для прогноза исхода популяции АС, поставляя в модель обобщенные характеристики популяции АС.
Для начала создадим модель простой логистической регрессии (у нас исход бинарный) с возрастом пациентов:
# STC
AB.IPD$y0 <- 1 - AB.IPD$y # Add in dummy non-event column
# Fit binomial GLM
STC.GLM <- glm(cbind(y,y0) ~ trt*I(age - AC.AgD$age.mean),
data = AB.IPD, family = binomial)
summary(STC.GLM)
Call:
glm(formula = cbind(y, y0) ~ trt * I(age - AC.AgD$age.mean),
family = binomial, data = AB.IPD)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.3774 -0.4877 0.3039 0.4733 2.0963
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.60576 0.27257 5.891 3.83e-09 ***
trtB -3.68237 0.41757 -8.819 < 2e-16 ***
I(age - AC.AgD$age.mean) 0.05747 0.02489 2.309 0.0209 *
trtB:I(age - AC.AgD$age.mean) -0.05690 0.03374 -1.686 0.0917 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 693.14 on 499 degrees of freedom
Residual deviance: 340.78 on 496 degrees of freedom
AIC: 348.78
Number of Fisher Scoring iterations: 5
Пробуем добавить в регрессионную модель пол пациентов:
Single term additions
Model:
cbind(y, y0) ~ trt * I(age - AC.AgD$age.mean)
Df Deviance AIC LRT Pr(>Chi)
<none> 340.78 348.78
gender 1 340.68 350.68 0.091053 0.7628
Как видно, добавление пола в модель не привело к существенному снижению остатков и увеличило значение AIC. Остановимся на модели с возрастами пациентов. Оценим logOR и дисперсию «В» в сравнении с «А» в популяции исследования АС:
print(d.AB.STC <- coef(STC.GLM)["trtB"])
trtB
-3.682373
print(var.d.AB.STC <- vcov(STC.GLM)["trtB","trtB"])
[1] 0.1743626
Выполняем финальный этап STC, проводим непрямое сравнение «С» в сравнение с «В» с учетом выше полученных результатов:
print(d.BC.STC <- d.AC - d.AB.STC)
-0.107572
print(var.d.BC.STC <- var.d.AC + var.d.AB.STC)
[1] 0.2983112
print(sqrt(var.d.BC.STC <- var.d.AC + var.d.AB.STC))
[1] 0.5461787
Таким образом, в результате STC получены следующие результаты:
- Эффект «С» в сравнении с «В» — logOR = -0.107572
- Стандартная ошибка среднего — 0.5461787
Результаты
Теперь, выполним расчет реальных значений logOR, проведем нескорректированное сравнение и изобразим результате на едином форест-плоте:
d.AB.TRUE <- b_trt_B + b_age_trt * (AC.AgD$age.mean - 40)
AB.IPD %>% group_by(trt) %>%
summarise(y.sum = sum(y)) %>%
spread(trt, y.sum) %>%
with({
d.AB.AB <<- log(B * (N_AB/2 - A) / (A * (N_AB/2 - B)))
var.d.AB.AB <<- 1/B + 1/(N_AB/2 - A) + 1/A + 1/(N_AB/2 - B)
})
d.BC.TRUE <- b_trt_C - b_trt_B
d.BC.NAIVE <- d.AC - d.AB.AB
var.d.BC.NAIVE <- var.d.AC + var.d.AB.AB
plotdat <- data_frame(
id = 1:10,
Comparison = factor(c(rep(1,4), 2, 2, rep(3,4)),
labels = c("B vs. A", "C vs. A", "C vs. B")),
Estimate = c(d.AB.TRUE, d.AB.MAIC, d.AB.STC, d.AB.AB,
b_trt_C + b_age_trt * (AC.AgD$age.mean - 40), d.AC,
d.BC.TRUE, d.BC.MAIC, d.BC.STC, d.BC.NAIVE),
var = c(NA, var.d.AB.MAIC, var.d.AB.STC, var.d.AB.AB,
NA, var.d.AC,
NA, var.d.BC.MAIC, var.d.BC.STC, var.d.BC.NAIVE),
lo = Estimate + qnorm(0.025) * sqrt(var),
hi = Estimate + qnorm(0.975) * sqrt(var),
type = c("True", "MAIC", "STC", "Unadjusted",
"True","Unadjusted",
"True", "MAIC", "STC", "Unadjusted")
)
ggplot(aes(x = Estimate, y = id, col = type, shape = type), data = plotdat) +
geom_vline(xintercept = 0, lty = 2) +
geom_point(size = 2) +
geom_segment(aes(y = id, yend = id, x = lo, xend = hi), na.rm = TRUE) +
xlab("Estimate (Log OR)") +
facet_grid(Comparison~., switch = "y", scales = "free_y", space = "free_y") +
scale_y_reverse(name = "Comparison in AC population", breaks = NULL, expand = c(0, 0.6))
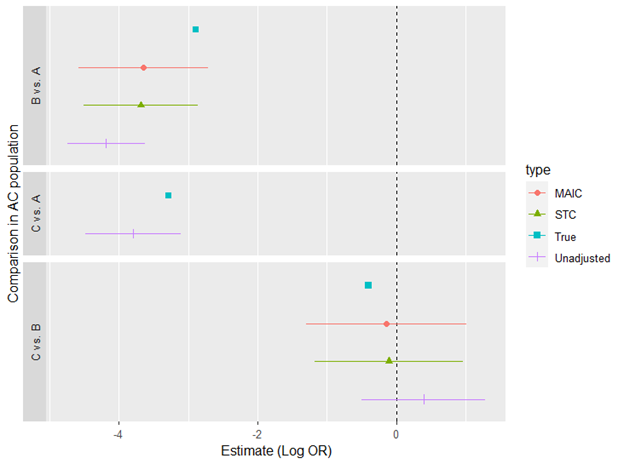
Следует отметить, что при воспроизведении всех вышеуказанных процедур в R вы получите отличающиеся результаты от представленных в материале. Это обусловлено тем, что генерация популяций пациентов происходит случайном образом в заданных пределах. В свою очередь, это повлияет на генерацию исходов. Код R из этого материала приложен ниже.
Дорогой читатель, буду рад твоим комментариям, предложениям и вопросам!