Привет, дорогой читатель и исследователь в области оценки технологий здравоохранения! В этом материале будет рассмотрено использование подключаемой библиотеки R – survHE. Это очень полезный инструмент, который объединяет в себе полный набор инструментов для анализа и моделирования выживаемости. Функциональные возможности:
- восстановление (псевдо) индивидуальных данных из оцифрованных кривых Каплана-Мейера
- подгонка различных моделей выживаемости с использованием различных методов (частотный анализ и метод Байеса)
- оценка и анализ подогнанных моделей
- выполнение вероятностного анализа чувствительности
- вывод данных для дальнейшей работы, например, в MS Excel
Ниже на рисунке представлены рабочие модули библиотеки survHE.
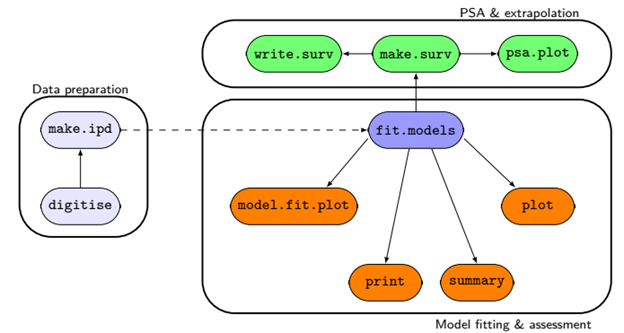
Использование этой библиотеки существенно сокращает количество кода R, которое необходимо написать при анализе выживаемости, что существенно сокращает сроки выполнения анализа. В итоге вы сможете сравнить количество кода – смотрите материал Восстановление (имитация) индивидуальных данных пациентов часть 2 и часть 3. Кроме того, есть удобная возможность использовать Байесовский метод при подгонке моделей. Но в данном материале мы будем использовать «классический» метод по умолчанию – оценка максимального правдоподобия (maximum likelihood estimation).
Очень рекомендую ознакомиться с публикацией, написанной создателем библиотеки survHE — Baio, G. (2020). survHE: Survival Analysis for Health Economic Evaluation and Cost-Effectiveness Modeling. Journal of Statistical Software, 95(14), 1–47.
Итак, начнем работу с библиотекой. В качестве исходных данных буду использовать результаты оцифровки кривой КМ. Вы можете его загрузить по ссылке ниже. Также, в материале Восстановление (имитация) индивидуальных данных пациентов часть 1 вы можете узнать, как выполнять оцифровку.
«Шапка» набора данных выглядит следующим образом:
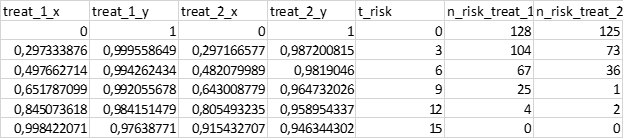
- treat_1_x – время, активная группа
- y – доля пациентов на достигших исхода, активная группа
- treat_2_x – время, контрольная группа
- treat_2_y – доля пациентов на достигших исхода, контрольная группа
- t_risk – временные отметки, для которых есть данные о количестве пациентов под риском
- n_risk_treat_1 – количество пациентов под риском на соответствующей временной отметке, активная группа
- n_risk_treat_2 – количество пациентов под риском на соответствующей временной отметке, контрольная группа
Устанавливаем и загружаем необходимые библиотеки:
install.packages("xlsx") # устанавливаем библиотеку для записи .xlsx файлов
install.packages("IPDfromKM") # устанавливаем библиотеку для восстановления IPD
install.packages("survHE") # устанавливаем библиотеку SurvHE
## Загружаем необходимые библиотеки ##
library(survHE)
library(IPDfromKM)
library(readr)
library(xlsx)
Загружаем данные, полученные в результате оцифровки рисунка кривой Каплана-Мейера:
digitizedKM <- read_delim("Digitized.csv",
delim = ";", escape_double = FALSE, col_types = cols(treat_1_y = col_double()),
locale = locale(decimal_mark = ","),
trim_ws = TRUE)
digitizedKM <- as.data.frame(digitizedKM) # переводим в формат датафрейма
head(digitizedKM) # смотрим верхнюю часть датафрейма
# treat_1_x treat_1_y treat_2_x treat_2_y t_risk n_risk_treat_1 n_risk_treat_2
# 1 0.0000000 1.0000000 0.0000000 1.0000000 0 128 125
# 2 0.2973339 0.9995586 0.2971666 0.9872008 3 104 73
# 3 0.4976627 0.9942624 0.4820800 0.9819046 6 67 36
# 4 0.6517871 0.9920557 0.6430088 0.9647320 9 25 1
# 5 0.8450736 0.9841515 0.8054932 0.9589543 12 4 2
# 6 0.9984221 0.9763877 0.9154327 0.9463443 15 0 0
Начинаем восстановление (имитацию) IPD:
## Выполняем препроцессинг результатов оцифровки ##
pre_treat_1 <- preprocess(dat = digitizedKM[,1:2], # 1-2 колонки - активная группа
trisk = digitizedKM$t_risk[1:6],
nrisk = digitizedKM$n_risk_treat_1[1:6], # кол-во под риском - активная группа
maxy = 1) # максимальное значение по оси У
pre_treat_2 <- preprocess(dat = digitizedKM[,3:4], # 3-4 колонки - контрольная группа
trisk = digitizedKM$t_risk[1:6],
nrisk = digitizedKM$n_risk_treat_2[1:6], # кол-во под риском - контрольная группа
maxy = 1) # максимальное значение по оси У
## Создаем псевдо IPD ##
ipd_treat_1 <- getIPD(prep = pre_treat_1,
armID = 1, # единица - активная группа
tot.events = NULL) # в публикации не было данных о кол-ве событий
ipd_treat_2 <- getIPD(prep = pre_treat_2,
armID = 0, # ноль - контрольная группа
tot.events = NULL) # в публикации не было данных о кол-ве событий
## Выгружаем IPD в отдельные переменные ##
ipd_active <- ipd_treat_1$IPD
ipd_control <- ipd_treat_2$IPD
## Переименовываем названия столбцов для работы в survHE ##
names(ipd_active)[names(ipd_active) == "status"] <- "event"
names(ipd_active)[names(ipd_active) == "treat"] <- "arm"
head(ipd_active) # проверяем название столбцов
# time event arm
# 1 0.3974983 0 1
# 2 0.4976627 1 1
# 3 0.7484304 0 1
# 4 0.8450736 1 1
# 5 0.9984221 1 1
# 6 1.0947580 0 1
names(ipd_control)[names(ipd_control) == "status"] <- "event"
names(ipd_control)[names(ipd_control) == "treat"] <- "arm"
head(ipd_control) # проверяем название столбцов
# time event arm
# 1 0.2971666 1 0
# 2 0.2971666 1 0
# 3 0.3896233 0 0
# 4 0.6359668 1 0
# 5 0.6430088 1 0
# 6 0.6935659 0 0
Библиотека позволяет за один раз подогнать множество моделей. В этом материале мы будем использовать 7 распределений для подгонки: экспоненциальное, гамма, генерализованное гамма, Гомпертца, Вейбулла, лог-логистическое, лог-нормальное. Запишем их в переменную models:
models <- c("exponential","gamma","gengamma","gompertz","weibull","loglogistic","lognormal")Запишем в отдельную переменную формулу для подгонки:
## Переменная, которая используется для подгонки (~ 1 - наши данные без модификаторов)
formula <- Surv(time, event) ~ 1Подгоняем и изучаем результаты для активной группы:
fitted_active <- fit.models(formula = formula, data = ipd_active, distr = models)
names(fitted_active$models) ## Названия моделей
# [1] "Exponential" "Gamma" "Gen. Gamma" "Gompertz" "Weibull (AFT)"
# [6] "log-Logistic" "log-Normal"
fitted_active$models$Gompertz ## смотрим результаты подгонки модель Гомпертца
# Call:
# flexsurv::flexsurvreg(formula = formula, data = data, dist = x)
#
# Estimates:
# est L95% U95% se
# shape 0.17621 0.10546 0.24697 0.03610
# rate 0.04286 0.02733 0.06720 0.00984
#
# N = 128, Events: 77, Censored: 51
# Total time at risk: 786.3896
# Log-likelihood = -244.671, df = 2
# AIC = 493.342
fitted_active$model.fitting ## смотрим goodness of fit - критерии AIC и BIC
# $aic
# [1] 513.8416 492.4919 492.8158 493.3420 491.2470 496.3148 498.5836
#
# $bic
# [1] 516.6937 498.1960 501.3719 499.0460 496.9510 502.0188 504.2876
#
# $dic
# NULL
Как видите, мы сразу же получили все необходимое для дальнейшего моделирования: коэффициенты, значения информационных критериев. Для этого потребовалось совсем небольшое количество строк кода.
Выполним аналогичную процедуру для контрольной группы и изучим другие функции библиотеки survHE:
## Выполняем аналогичные процедуры для контрольной группы
fitted_control <- fit.models(formula = formula, data = ipd_control, distr = models)
names(fitted_control$models)
fitted_control$models$Gompertz
fitted_control$model.fitting
Визуализируем полученные оценки подогнанных моделей AIC и BIC:
## Оцениваем goodness of fit (степень соотвествия модели и исходных данных)
## Активная группа ##
model.fit.plot(fitted_active) ## наименьший AIC у модели Вейбулла
model.fit.plot(fitted_active, type = "bic") ## наименьший BIC у модели Вейбулла
model.fit.plot(fitted_active, scale = "relative") ## смотрим на относительной шкале
model.fit.plot(fitted_active, scale = "relative", col = "pink") ## меняем цвет
## Контрольная группа ##
model.fit.plot(fitted_control) ## наименьший AIC у логнормального распределения
model.fit.plot(fitted_control, type = "bic") # наименьший BIC у логнормального распределения
model.fit.plot(fitted_control, scale = "relative") ## смотрим на относительной шкале
model.fit.plot(fitted_control, scale = "relative", col = "pink") ## меняем цвет
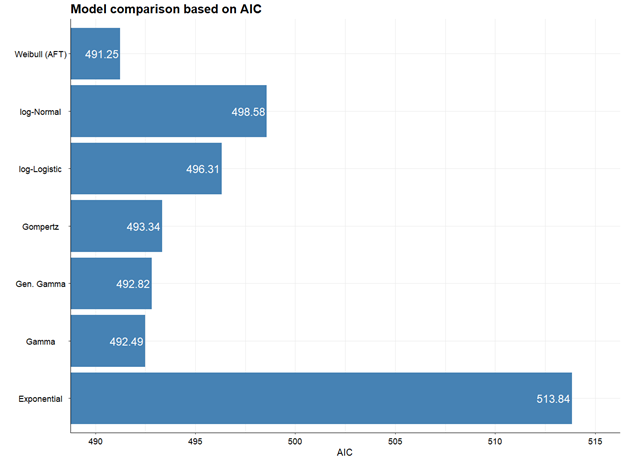
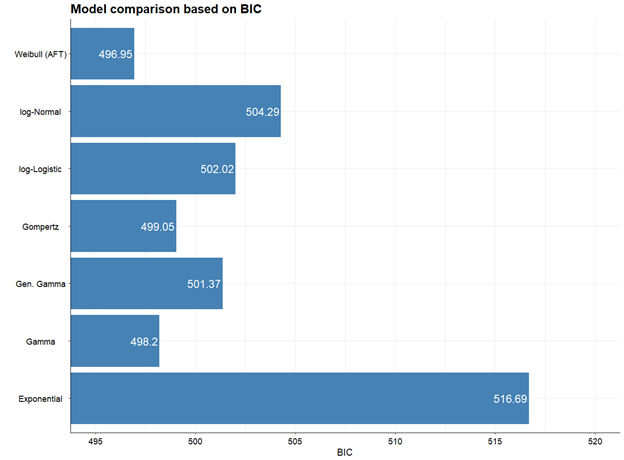
Наименьшее значение AIC и BIC для активной группы имеет модель Вейбулла, для контрольной – лог-нормальное распределение.
Выводим результаты на графиках:
## Выводим графики ##
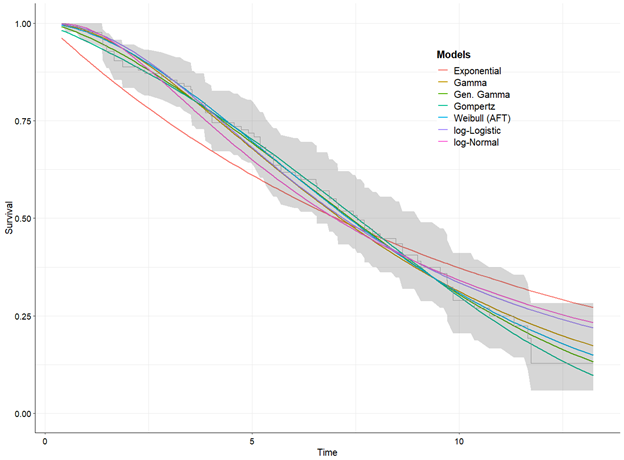
plot(fitted_active, add.km = T) # add.km - добавляем кривую Каплан-Мейера
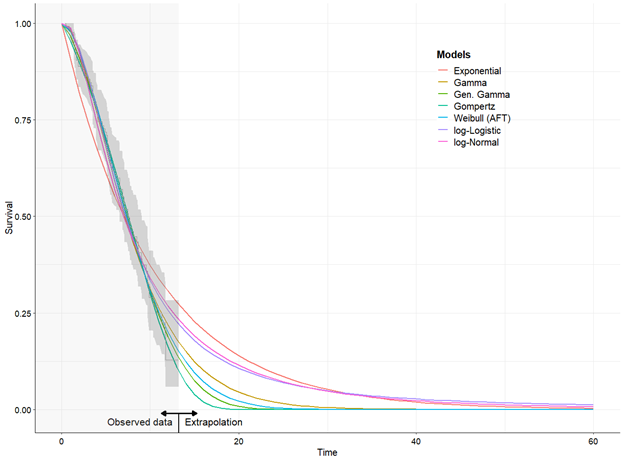
plot(fitted_active, add.km = T, annotate = T, t = seq(0, 60)) # увеличиваем время
plot(fitted_active, add.km = T, annotate = T, t = seq(0, 60), mods = 5) # лучшая модель по AIC и BIC для активной группы, mods = 5 - номер модели по счету в переменной models
plot(fitted_control, add.km = T, annotate = T, t = seq(0, 60), mods = 7) # лучшая модель по AIC и BIC для контрольной группы группы, mods = 7 - номер модели по счет в переменной models
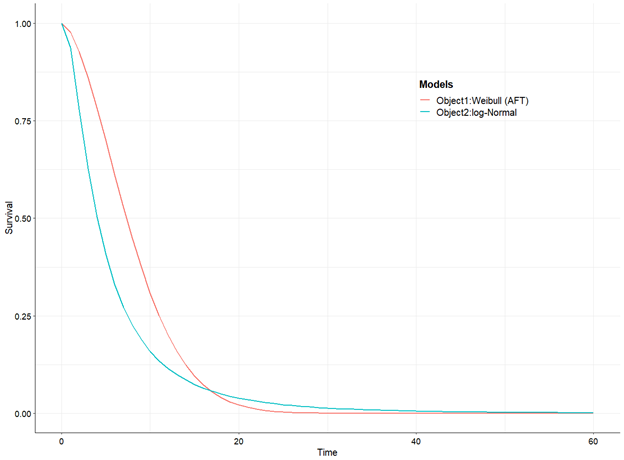
plot(fitted_active, fitted_control, mods = c(5, 14), t = seq(0, 60)) # "лучшие" модели на одном графике, mods = c(5, 14) - номер необходимых моделей по счету
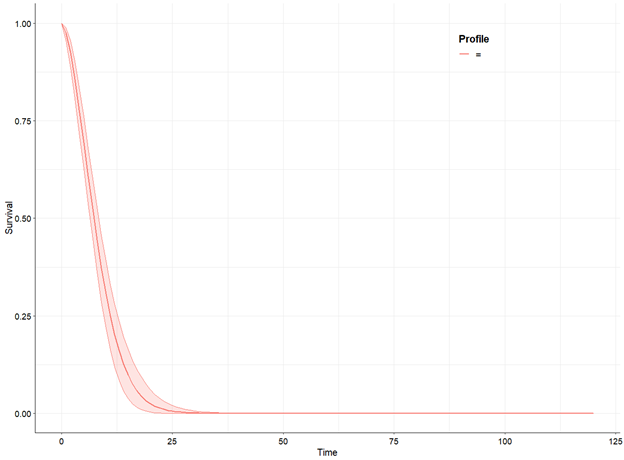
Также, можно выполнить вероятностный анализ чувствительности полученных результатов и выгрузить итерации анализа чувствительности в файл формата MS Excel для дальнейшей работы:
## Выполняем вероятностный анализ чувствительности ##
psa_active <- make.surv(fit = fitted_active, mod = 5, nsim = 1000, t = seq(0, 120))
names(psa_active)
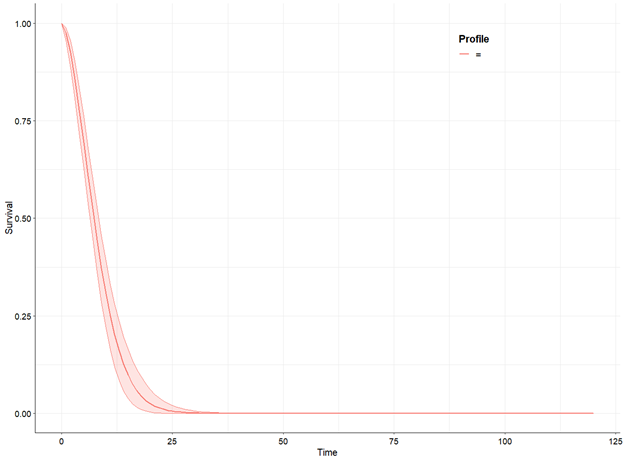
psa.plot(psa_active)
psa_control <- make.surv(fit = fitted_control, mod = 7, nsim = 1000, t = seq(0, 120))
psa.plot(psa_control)
## Записываем результаты АЧ в файл MS Excel ##
write.surv(psa_active, file = "active_from_R.xlsx")
Дорогие читатели, в этом материале мы познакомились с библиотекой survHE, которая сильно упрощает и ускоряет анализ выживаемости для фармакоэкономических моделей.
Ниже вы найдете файл с кодом R данного материала.
В части 3 материала Восстановление (имитация) индивидуальных данных пациентов Вы найдете макрос MS Excel с формулами общей выживаемости для различных распределений.
Дорогой читатель, буду рад твоим комментариям, предложениям и вопросам!