Привет, дорогой читатель! Рад тебя приветствовать в третей и последней части материала, посвященного восстановлению (имитации) индивидуальных данных пациентов из опубликованных результатов клинических исследование в виде кривых Каплан-Мейера.
В первой части мы разобрали процедуру оцифровки кривых Каплан-Мейера из опубликованного источника.
Во второй части мы выполнили непосредственно процедуру восстановления (имитации) пациентских данных в клиническом исследовании и получили очень близкие к оригинальным результаты:
- оригинальные – HR 0,37 (95% ДИ 0,18-0,77), р = 0,004
- восстановленные – HR 0,3765 (95% ДИ 0,1855-0,764), р = 0,00682
Если бы я потратил больше времени на более тщательную оцифровку кривых, уверен, результаты были бы еще ближе к оригинальным.
В последней третей части этого материалы мы на практике выполним подгонку параметрических моделей к восстановленным данным, выполним оценку адекватности подгонки (goodness of fit) моделей с помощью информационных критериев Акаике (AIC — Akaike information criterion) и Байеса (BIC — Bayesian information criterion), сделаем предположения о долгосрочной общей выживаемости в случае применение нусинерсена для терапии спинальной мышечной атрофии в сравнении с плацебо (sham control) на основании полученных параметрических моделей.
Для начала загружаем и устанавливаем необходимую библиотеку R для подгонки параметрической модели – flexsurv.
install.packages("flexsurv")
library(flexsurv)
Для подгонки модели будем использовать следующие распределения: Вейбулла, Гомпертца, лог-логистическое, логнормальное, генерализованное (обобщенное) гамма и экспоненциальное.
В результате восстановления данных мы получили два объекта:
- est_arm_0 – восстановленные данные для группы плацебо
- est_arm_1 – восстановленные данные для группы нусинерсена
Необходимые для параметрической модели данные в формате «время-статус» находятся в дата фрейме $IPD вышеуказанных объектов:
> head(est_arm_0$IPD)
time status treat
1 2.952085 1 0
2 2.952085 1 0
3 5.090194 1 0
4 5.123424 1 0
5 5.369344 1 0
6 10.465369 1 0
> head(est_arm_1$IPD)
time status treat
1 0.8229476 1 1
2 5.2361236 1 1
3 6.3180365 1 1
4 6.4382490 0 1
5 7.8807996 1 1
6 8.6621811 1 1
С помощью функции flexsurvreg начнем подгонять параметрические модели с группы нусинерсена (arm_1). Подробно рассмотрим формулу на примере распределения Вейбулла.
flex_weibull_1 <- flexsurvreg(Surv(est_arm_1$IPD$time, #создаем survival object (библиотека survival), где первый аргумент - время
est_arm_1$IPD$status) ~ 1, #второй аргумент – статус. ~1 означает, что в наших данных нет (в данном случае) или мы не анализируем модификаторы (например пол, возраст и т.д.)
dist = "weibull") #указываем необходимое распределение
Изучаем полученную модель:
> flex_weibull_1
Call:
flexsurvreg(formula = Surv(est_arm_1$IPD$time, est_arm_1$IPD$status) ~
1, dist = "weibull")
Estimates:
est L95% U95% se
shape 0.766 0.468 1.256 0.193
scale 354.080 99.507 1259.937 229.306
N = 80, Events: 14, Censored: 66
Total time at risk: 3004.692
Log-likelihood = -88.54557, df = 2
AIC = 181.0911
shape и scale – коэффициенты распределения Вейбулла
AIC – значение информационного критерия Акаике
Выводим график полученной параметрической модели:
plot(flex_weibull_1)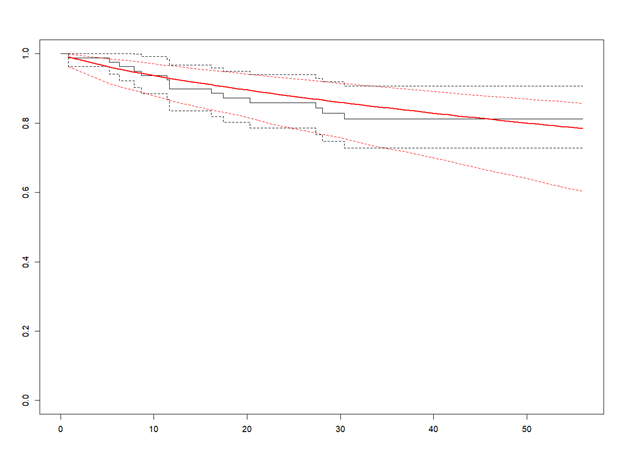
- Сплошная черная линия – кривая Каплана-Мейера
- Сплошная красная линия – кривая параметрической модели с применением распределения Вейбулла
- Пунктирные линии – 95% ДИ
Ниже приведен код аналогичной процедуры для остальных распределений, которые были озвучены ранее, а также, для группы плацебо.
flex_gompertz_1 <- flexsurvreg(Surv(est_arm_1$IPD$time, est_arm_1$IPD$status) ~ 1,
dist = "gompertz")
flex_llogis_1 <- flexsurvreg(Surv(est_arm_1$IPD$time, est_arm_1$IPD$status) ~ 1,
dist = "llogis")
flex_lnorm_1 <- flexsurvreg(Surv(est_arm_1$IPD$time, est_arm_1$IPD$status) ~ 1,
dist = "lnorm")
flex_gengamma_1 <- flexsurvreg(Surv(est_arm_1$IPD$time, est_arm_1$IPD$status) ~ 1,
dist = "gengamma")
flex_exp_1 <- flexsurvreg(Surv(est_arm_1$IPD$time, est_arm_1$IPD$status) ~ 1,
dist = "exp")
flex_weibull_0 <- flexsurvreg(Surv(est_arm_0$IPD$time, est_arm_0$IPD$status) ~ 1,
dist = "weibull")
flex_gompertz_0 <- flexsurvreg(Surv(est_arm_0$IPD$time, est_arm_0$IPD$status) ~ 1,
dist = "gompertz")
flex_llogis_0 <- flexsurvreg(Surv(est_arm_0$IPD$time, est_arm_0$IPD$status) ~ 1,
dist = "llogis")
flex_lnorm_0 <- flexsurvreg(Surv(est_arm_0$IPD$time, est_arm_0$IPD$status) ~ 1,
dist = "lnorm")
flex_gengamma_0 <- flexsurvreg(Surv(est_arm_0$IPD$time, est_arm_0$IPD$status) ~ 1,
dist = "gengamma")
flex_exp_0 <- flexsurvreg(Surv(est_arm_0$IPD$time, est_arm_0$IPD$status) ~ 1,
dist = "exp")
Для того, чтобы оценить значения BIC, Байесовского информационного критерия, используем функцию BIC библиотеки stats.
library(stats)
BIC(flex_weibull_1)
[1] 185.8552
Итак, в настоящий момент мы получили все необходимые данные для выбранных распределений, которые мы хотим применить для создания параметрических моделей: коэффициенты распределений, значения AIC и BIC. Теперь можно переносить все эти данные в Эксель. Получаем следующую таблицу:
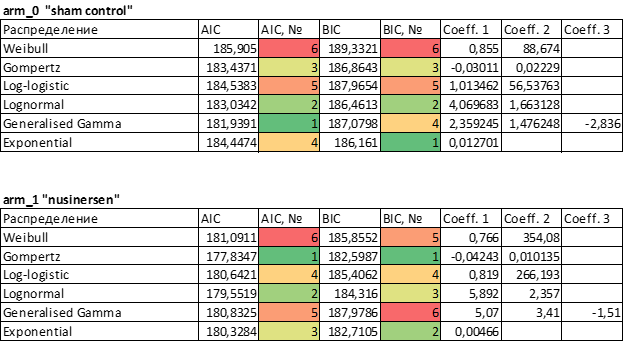
Оценим адекватность подгонки моделей (goodness of fit) с помощью информационных критериев AIC и BIC. Модели с наименьшим значением являются наиболее соответствующими исходному набору данных. В группе плацебо наилучшей по AIC является модель с использованием генерализованного гамма распределения, по BIC – экспоненциальное распределение. В группе нусинерсена по AIC и BIC – распределение Гомпертца.
Теперь представим результаты на графиках. Для расчетов с применением различных распределений я использую пользовательскую функцию, написанную в Visual Basic:
Public Function Fnc_Survival(ByVal strDist As String, _
ByVal dblTime As Double, _
ByVal dblSurvParam1 As Double, _
Optional ByVal dblSurvParam2 As Double = 0, _
Optional ByVal dblSurvParam3 As Double = 0) As Double
'Finds appropriate distribution and calculates the events based on distribution
If dblTime = 0 Then
Fnc_Survival = 1
ElseIf strDist = "Weibull" Then
Fnc_Survival = 1 - Application.WorksheetFunction.Weibull_Dist(dblTime, dblSurvParam1, dblSurvParam2, True)
ElseIf strDist = "Log-logistic" Then
Fnc_Survival = (1 / (1 + (dblTime / dblSurvParam2) ^ dblSurvParam1))
ElseIf strDist = "Lognormal" Then
Fnc_Survival = (1 - Application.WorksheetFunction.LogNorm_Dist(dblTime, dblSurvParam1, dblSurvParam2, True))
ElseIf strDist = "Gompertz" Then
Fnc_Survival = Exp(dblSurvParam2 / dblSurvParam1 * (1 - Exp(dblSurvParam1 * dblTime)))
ElseIf strDist = "Gamma" Then
Fnc_Survival = 1 - Application.WorksheetFunction.GammaDist(dblTime, dblSurvParam1, 1 / dblSurvParam2, True)
ElseIf strDist = "Generalised Gamma" Then
If dblSurvParam3 > 0 Then
Fnc_Survival = (1 - Application.WorksheetFunction.GammaDist(((-dblSurvParam3) ^ (-2)) * Exp((-dblSurvParam3) * (-((Log(dblTime) - dblSurvParam1) / dblSurvParam2))), _
(-dblSurvParam3) ^ (-2), 1, True))
ElseIf dblSurvParam3 <= 0 Then
Fnc_Survival = Application.WorksheetFunction.GammaDist(((-dblSurvParam3) ^ (-2)) * Exp((-dblSurvParam3) * (-((Log(dblTime) - dblSurvParam1) / dblSurvParam2))), _
(-dblSurvParam3) ^ (-2), 1, True)
End If
Else
Fnc_Survival = 0
End If
End Function
В этой функции:
- 1-ый аргумент – название распределения (указывать в “”)
- 2-ой аргумент – время
- 3-ий аргумент – коэффициент распределения № 1
- 4-ый аргумент — коэффициент распределения № 2 (если не используется, оставить пустым)
- 5-ый аргумент — коэффициент распределения № 3 (если не используется, оставить пустым)
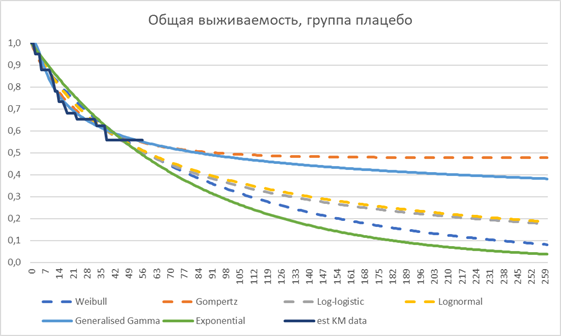
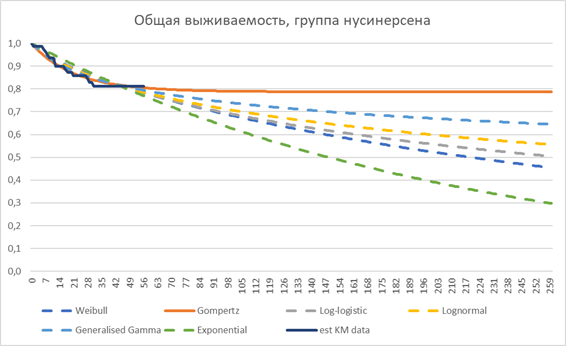
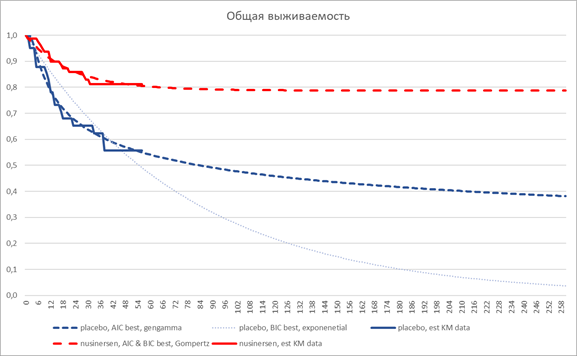

Как видим, выбор распределения существенно влияет на прогноз общей выживаемости за горизонтом наблюдения в клиническом исследовании. При этом, критерии AIC и BIC не являются определяющими. Экспоненциальное распределение, которое оказалось лучшим по BIC для группы плацебо при визуальном контроле оказывается совершенно неподходящим. Оптимальным при выборе модели является их валидации с помощью других данных, которые имеются в наличии, а также с привлечением экспертного мнения. Более подробно этот вопрос описан в NICE DSU TSD 14.
На этом завершу последнюю третью часть материала, посвященного восстановлению и экстраполяции индивидуальных данных пациентов из опубликованных кривых Каплана-Мейера. Многое осталось «за бортом» этого материала, но основные моменты постарался отразить, сделав акцент на практической части, а именно какие нужны для этого утилиты и как выполнить все процедуры.
Ниже приложил файлы с кодом R и Эксель с результатами.
Дорогой читатель, буду рад твоим комментариям, предложениям и вопросам!